JPEG phase awareness revisited

When a JPEG image is decompressed to the spatial domain, the statistical properties of the pixels depend on their spatial location within the JPEG grid, the so-called JPEG phase.

Careful consideration of the JPEG phase is a key property in modern JPEG steganalysis feature descriptors, such as the DCT residuals (DCTR), the phase-aware projection model (PHARM), and the Gabor filter residual (GFR) features. This blog post explains the JPEG phase and how PHARM exploits symmetries in decompressed JPEG images to reduce the feature dimensionality.

Perceiving the JPEG phase

The JPEG phase can be perceived by comparing histograms of pixel values from varying spatial locations. For illustration, we take 10.000 uncompressed images from the BOSSBase and compress them with JPEG quality close to 75. To focus on the effects of JPEG compression, we isolate the compression changes by subtracting the uncompressed image from the decompressed image. The compression changes are split into non-overlapping 8x8 blocks, from which we calculate 64 histograms, one for each “mode” in the 8x8 grid.

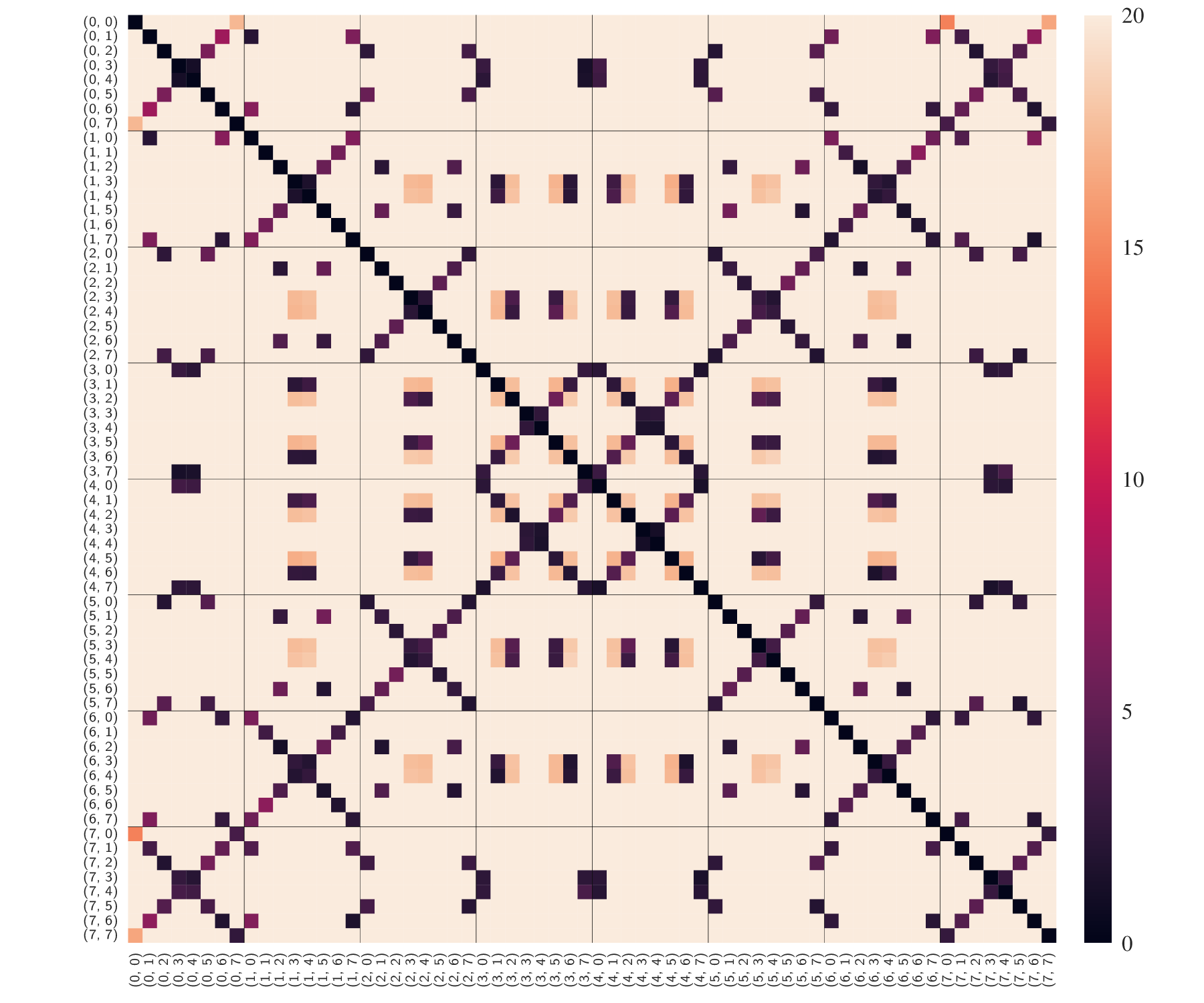
The figure above shows the pairwise L1 distances between histograms calculated from each of the 64 modes. Dark colors represent small distances, light colors represent high distances. The ticks indicate the modes (i, j), where i is the row index and j is the column index. It can be seen that the individual modes are the most similar to their horizontally or vertically flipped modes, i.e., mode (i, j) is most similar to modes (i, 7-j), (7-i, j), and (7-i, 7-j). For example, the histogram for mode (2, 0) is similar to the modes (2, 7) (horizontal flip), (5, 0) (vertical flip), and (5, 7) (horizontal + vertical flip). To some extent, modes are also similar to locations obtained by transposition and rotation by multiples of 90 degrees. For example, the histogram at location (2, 0) resembles the histograms at modes (0, 2), (0, 5), (7, 2), and (7, 5), which are obtained by transposition and rotation.

Besides these symmetries, observe the dissimilarity between two arbitrary selected modes! The high dissimilarity suggests that first-order statistics calculated from decompressed images should be carefully split by their location w.r.t. the JPEG grid. This is key innovation of the phase-aware projection model (PHARM), a popular steganalysis feature vector. PHARM extends the previous projection spatial rich model (PSRM) by the phase awareness. Instead of averaging over projections at arbitrary locations, the projections are carefully split by the JPEG phase. This blog post focuses on the symmetrization. More details about PHARM can be found in the corresponding conference publication by Vojtěch Holub and Jessica Fridrich.

PHARM symmetrization

Many steganalysis features exploit the symmetries of natural images that we have observed above. These symmetries allow combining histograms from symmetric locations, thereby reducing the feature descriptor’s dimensionality and improving its statistical robustness.

PHARM exploits flipping symmetries. Figure 1 in the original paper illustrates the symmetrization in the residual domain. For implementation purposes, it is helpful to draw both the decompressed domain and the residual domain. For simplicity, we assume that the projection kernel has size 1x1.

The left figure shows pixels in the decompressed domain with the block boundaries. The right figure shows the residual domain. Let’s say the residual was obtained by convolving the decompressed image with a 1x2 filter kernel. This means that two horizontally adjacent pixels in the decompressed image contribute to one residual pixel. For example, the blue circle in the residual domain (right) is obtained from the two pixels in the decompressed domain (left, blue box).

In order to exploit flipping symmetries in the residual domain, we need to keep track of which pixels in the decompressed image contributed to the residual pixel. The calculation involves the filter kernel’s height and width. Similar to how the blue box aligns with the 8x8 block’s top-left corner, the horizontally flipped counterpart should align with the blocks’ top-right corner, as shown by the yellow box. The corresponding residual pixel (yellow circle) is at the spatial offset (0, 6). Note that the offset (0, 7) would correspond to a pair of decompressed pixels that crosses the block boundary. The locations obtained from vertical flipping are colored in light orange. Horizontal and vertical flipping leads to the dark orange pixels. The grey circles correspond to the same locations in neighboring blocks.

Based on these symmetries, we obtain four very similar histograms. The symmetrization reduces these four to one.

Steganalysis

In this final section, we evaluate the steganalysis performance of the PHARM features using the following experimental setup. The 10.000 BOSSBase images are JPEG-compressed with libjpeg-turbo 2.1.0 and quality factor 75. We use the JPEG steganography method J-UNIWARD to embed 0.4 bit per non-zero AC coefficient into each image. For all cover and stego images, the PHARM features are extracted with the quantization step q = 4 and truncation threshold T = 3, which gave slightly better results in this experimental setup than the parameters used in the paper. After randomly splitting the 10.000 images into 5.000 cover-stego pairs for training and 5.000 for testing, an ensemble classifier with Fisher linear discriminant base learners is trained on the training set and its accuracy is evaluated on the test set. The random splitting and training is repeated four more times and the results are averaged over the five splits.

The figure above shows the steganalysis performance with and without symmetrization as a function of the number of projections. The non-symmetrized variant does not compute the flipped histograms, thus both variants have the same number of dimensions. As expected, a higher number of projections gives higher accuracy, but also increases the computational cost of the feature extraction and the feature dimensionality. With 800 projections, the PHARM features with symmetrization attain an accuracy of 89.2% while the non-symmetrized variant only attains 85.7%. The symmetrization gives a consistent gain in accuracy by 3 to 6%-pts. The gain is the highest when the number of projections is small. The performance gap decreases as the number of projections increases. These results confirm the benefits of the symmetrization.

Conclusion

In JPEG images, the pixel statistics depend on their relative location w.r.t. the JPEG grid. The PHARM features carefully account for the JPEG phase, which makes them outperform previous phase-unaware features. Incorporating symmetries of JPEG images into the PHARM features improves the steganalysis performance by 3 to 6%-pts.